분할표(Contingency Table)는 명목형(Categorical) 또는 순서형(Ordinal) 데이터의 도수(frequency)를 표 형태로 기록한 것이다. 분할표가 작성되면 카이 제곱 검정(Chi Square Test)으로 변수 간에 의존 관계가 있는지를 독립성 검정으로, 도수가 특정 분포를 따르는지를 적합도 검정(Goodness of Fit)으로 살펴볼 수 있다.
분할표가 사용되는 한 가지 경우는 기계 학습으로 데이터의 양성(Positive), 음성(Negative)을 예측할 때다. 예를 들어, 이메일 텍스트를 보고 해당 이메일이 스팸인지 아닌지를 예측하는 경우를 생각해보자. 이때 두 가지 변수는 예측값(모델로 스팸인지를 판단한 결과)과 실제 값(실제로 해당 이메일이 스팸인지 여부)이다. 이런 실험에서 분할표의 모양은 다음과 같다.
| 예측-스팸 | 예측-스팸 아님 | |
| 실제-스팸 | a | b |
| 실제-스팸 아님 | c | d |
표에서 a는 주어진 이메일이 실제로 스팸일 때 모델의 예측 결과도 스팸인 경우의 수다. b는 실제로 스팸인데 예측은 스팸이 아니라고 된 경우다. c와 d도 유사하게 해석할 수 있다.
분할표 작성
분할표를 작성하는 함수에는 table(), xtabs()가 있다. table()은 "최빈값" 절에서 보인 바 있다. 여기서는 xtabs()를 주로 살펴본다.
-xtabs : 포뮬러를 사용해 분할표를 작성한다.
xtabs(
formula, # L1 ~ R1 + R2 + R3 형태의 포뮬러다. R1, R2, R3 등은 분할표의 분류를
# 나타내는 변수들이다. "~"의 왼쪽에 빈도를 나타내는 변수를 적을 수 있다.
data, # 포뮬러를 적용할 데이터
)
다음은 table()을 사용해 주어진 벡터에서 a, b, c의 출현 횟수를 세는 간단한 예다.
| >table(c("a", "b", "b", "b", "c", "c", "d")) a b c d 1 3 2 1 |
xtabs()는 포뮬러를 사용해 데이터를 지정할 수 있다. 예를 들어, x, y라는 두 변수가 있고 (x, y)에 대한 도수가 num에 저장되어 있을 때, 이 데이터로부터 분할표를 만드는 포뮬러는 num ~ x + y다. 다음은 이 포뮬러를 사용해 분할표를 작성하는 예다.
| >d<-data.frame(x=c("1", "2", "2", "1"), + y=c("A", "B", "A", "B"), + num=c(3, 5, 8, 7)) >(xtabs(num ~ x + y, data=d)) y x A B 1 3 7 2 8 5 |
만약 도수를 나타내는 컬럼이 따로 없고, 각 관찰 결과가 서로 다른 행으로 표현되어 있다면 ‘~ 변수 + 변수 …’ 형태로 포뮬러를 작성한다. 다음 코드는 x 값이 A 또는 B인 각 경우의 수를 세는 예를 보여준다.
| >(d2<-data.frame(x=c("A", "A", "A", "B", "B"))) x 1 A 2 A 3 A 4 B 5 B >(xtabs(~ x, d2)) x A B 3 2 |
합, 비율의 계산
여러 변수가 있을 때 한 변수만을 기준으로 총계를 구하는 경우를 생각해보자. 예를 들어, 다음은 변수 A, B에 대한 분할표다. 각 변수는 True, False 값을 가질 수 있다. 이 표에는 변수 B가 True, False인 경우의 합(100과 90)을 표시한 컬럼과, 변수 A가 True, False일 때 합을 표시한 총계 행(80과 110)이 표시되어 있다. 또, 전체 도수의 합 역시 표시되어 있다. 이러한 총계 컬럼 또는 행을 주변 합(marginal sum)이라고 한다. ‘주변’이란 데이터가 표시된 바깥쪽 행 또는 열에 값이 기록되기에 붙여진 이름이다.
| 변수A-True | 변수A-False | 통계 | |
| 변수B-True | 30 | 70 | 100 |
| 변수B-False | 50 | 40 | 90 |
| 통계 | 80 | 110 | 190 |
주변 합이 계산되고 나면 이를 기준으로 비율을 계산할 수 있다. 예를 들어, 다음은 위에 보인 표에서 변수 B의 합을 기준으로 비율을 계산한 결과다.
| 변수A-True | 변수A-False | |
| 변수B-True | 0.3 (= 30/100) | 0.7 (= 70/100) |
| 변수B-False | 0.56 (= 50/90) | 0.44 (= 40/90) |
마찬가지로 변수 A의 합을 기준으로 비율을 구하거나 전체 데이터의 총 빈도(190)를 기준으로 비율을 계산할 수도 있다.
주변 합과 주변 비율은 margin.table(), prop.table()로 계산한다.
-margin.table : 분할표의 주변 합을 구한다.
margin.table(
x, # 배열
# 색인 번호. 1은 행 방향, 2는 열 방향을 뜻한다. 기본값인 NULL은 전체 값의 합을 구한다.
margin=NULL
)
-prop.table : 분할표의 주변 비율을 구한다.
prop.table(
x,
margin=NULL
)
다음은 margin.table()을 사용해 행 방향, 열 방향의 합과 전체 합을 구한 예다.
| >xt<-(xtabs(num ~ x + y, data=d)) >xt y x A B 1 3 7 2 8 5 >margin.table(xt, 1) # 3 + 7 = 10, 8 + 5 = 13 x 1 2 10 13 >margin.table(xt, 2) # 3 + 8 = 11, 7 + 5 = 12 y A B 11 12 >margin.table(xt) # 3 + 7 + 8 + 5 = 23 [1] 23 |
prop.table( )은 분할표로부터 각 셀의 비율을 계산한다. 호출 형식은 margin.table()의 경우와 동일하다.
| > xt y x A B 1 3 7 2 8 5 >prop.table(xt, 1) # xt의 각 행을 각각 10(= 3 + 7), 13(= 8 + 5)로 나눈 값 y x A B 1 0.3000000 0.7000000 2 0.6153846 0.3846154 >prop.table(xt, 2) # xt의 각 열을 각각 11(= 3 + 8), 12(= 7 + 5)로 나눈 값 y x A B 1 0.2727273 0.5833333 2 0.7272727 0.4166667 >prop.table(xt) # xt의 각 셀을 전체 데이터의 합 23(= 3 + 7 + 8 + 5)로 나눈 값 y x A B 1 0.1304348 0.3043478 2 0.3478261 0.2173913 |
독립성 검정
분할표의 행에 나열된 변수와 열에 나열된 변수가 독립이라고 가정하자. 만약 분할표에서 행과 열이 독립이라면 (i, j) 셀의 확률 P(i, j)에 대해 다음 식이 성립한다.

예를 들어, 다음 분할표를 생각해보자.
| 변수A-True | 변수A-False | 통계 | |
| 변수B-True | 30 | 70 | 100 |
| 변수B-False | 50 | 40 | 90 |
| 통계 | 80 | 110 | 190 |
표에서 변수 A가 True일 확률은 80/190, 변수 A가 False일 확률은 70/190이다. 마찬가지로 변수 B가 True일 확률은 100/190, 변수 B가 False일 확률은 90/190이다. 따라서 만약 A와 B가 독립이라면 변수 A가 True이고, 변수 B가 True일 확률은 (80/190) * (100/190)이라고 할 수 있다. 독립성 검정(Independence Test)은 실제로 이와 같은 가정이 성립하는지 알아보는 것을 목표로 한다.
변수 간의 독립성 검정에는 카이 제곱 검정(Chi-Squared Test)을 사용하며, 이때 사용되는 통계량은 다음과 같다.
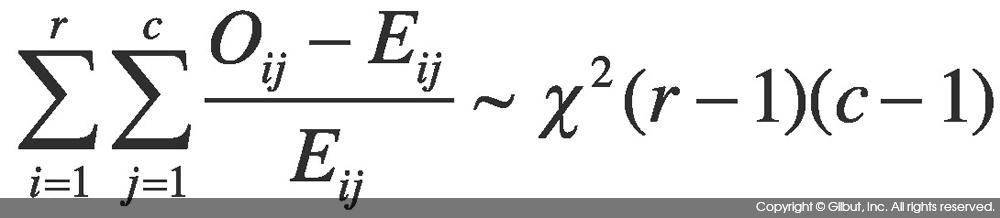
위 식에서 r은 행의 수, c는 열의 수를 의미한다. Oij는 분할표의 (i, j) 셀에 기록되어 있는 값이며, 분할표를 보면 바로 알 수 있는 값이다. Eij는 분할표의 두 변수가 독립일 때 (i, j) 셀에 대한 기댓값이다. 식 7-1에 의해 전체 데이터의 수가 n이라 할 때 Eij = n×P(i, j) = n×P(i)×P(j)다.
학생 설문 조사 데이터를 담고 있는 MASS::survey를 사용해 학생들의 성별에 따른 운동량에 차이가 있는지 독립성 검정을 해보자. 다음은 survey 데이터의 모양을 보여준다.
| >library(MASS) >data(survey) >str(survey) 'data.frame': 237 obs. of 12 variables: $ Sex : Factor w/ 2 levels "Female","Male": 1 2 2 2 2 1 2 1 2 2 ... $ Wr.Hnd: num 18.5 19.5 18 18.8 20 18 17.7 17 20 18.5 ... $ NW.Hnd: num 18 20.5 13.3 18.9 20 17.7 17.7 17.3 19.5 18.5 ... $ W.Hnd : Factor w/ 2 levels "Left","Right": 2 1 2 2 2 2 2 2 2 2 ... $ Fold : Factor w/ 3 levels "L on R","Neither",..: 3 3 1 3 2 1 1 3 3 3 ... $ Pulse : int 92 104 87 NA 35 64 83 74 72 90 ... $ Clap : Factor w/ 3 levels "Left","Neither",..: 1 1 2 2 3 3 3 3 3 3 ... $ Exer : Factor w/ 3 levels "Freq","None",..: 3 2 2 2 3 3 1 1 3 3 ... $ Smoke : Factor w/ 4 levels "Heavy","Never",..: 2 4 3 2 2 2 2 2 2 2 ... $ Height: num 173 178 NA 160 165 ... $ M.I : Factor w/ 2 levels "Imperial","Metric": 2 1 NA 2 2 1 1 2 2 2 ... $ Age : num 18.2 17.6 16.9 20.3 23.7 ... >head(survey[c("Sex", "Exer")]) Sex Exer 1 Female Some 2 Male None 3 Male None 4 Male None 5 Male Some 6 Female Some |
survey 데이터에서 성별은 Sex, 운동을 얼마나 하는지는 Exer 열에 저장되어 있다. Sex는 Female, Male 두 가지 레벨을 가지는 팩터이며, Exer는 Freq, Some, None 3가지 레벨로 구성된 팩터이다. Freq는 운동을 자주함, Some은 운동을 약간 함, None은 운동을 하지 않음을 의미한다.
성별과 운동이 독립인지를 확인해보기 위해 분할표를 만들어보자.
| >xtabs(~ Sex + Exer, data=survey) Exer Sex Freq None Some Female 49 11 58 Male 65 13 40 |
분할표를 작성하고 나면 chisq.test()를 통해 카이 제곱 검정을 수행할 수 있다.
-chisq.test : 카이 제곱 검정을 수행한다.
chisq.test(
x, # 숫자 벡터 또는 행렬. 또는 x와 y가 모두 팩터
y=NULL, # 숫자 벡터 또는 x가 팩터인 경우 팩터로 지정. x가 행렬인 경우 그 안에 분할표가
# 저장되어 있는 경우므로 y가 무시된다.
# x와 같은 길이를 가질 확률. 이 값이 비율이 이 확률과 같은지를 테스트한다. 이 값이 지정되지
# 않으면 확률이 서로 같은지 테스트한다. 이 인자는 '7.5 적합도 검정' 절에서 사용법을 설명한다.
p = rep(1/length(x), length(x))
)
다음은 성별과 운동 정도의 독립성 검정을 수행한 예다.
| >chisq.test(xtabs(~ Sex + Exer, data=survey)) Pearson's Chi-squared test data: xtabs(~Sex + Exer, data = survey) X-squared = 5.7184, df = 2, p-value = 0.05731 |
p 값이 0.05731이므로 0.05보다 커서 ‘H0: 성별과 운동은 독립이다.’라는 귀무가설을 기각할 수 없는 것으로 나타났다. 통계량 χ2은 5.7184였으며 자유도(Degree of Freedom)는 성별이 2개 레벨, 운동량이 3개 레벨이므로 (2-1)(3-1) = 2였다.
피셔의 정확 검정
분할표를 그린 뒤 카이 제곱을 적용할 때 표본 수가 적거나 표본이 분할표의 셀에 매우 치우치게 분포되어 있다면 카이 제곱 검정의 결과가 부정확할 수 있다. 표본 수가 적다는 기준은 특정 짓기 어렵지만 기대 빈도가 5 이하인 셀이 전체의 20% 이상인 경우 등이 이에 해당한다. chisq.test()는 이런 경우 경고 메시지를 출력하여 카이 제곱 검정이 부정확할 수 있음을 알린다.
카이 제곱 검정이 부정확한 경우에는 피셔의 정확 검정(Fisher’s Exact Test)을 사용한다. 통계적인 계산식에 대한 설명은 피셔의 정확한 검정에 대한 참고자료를 보기 바란다. 이 절에서는 R에서 피셔의 정확 검정을 수행하는 방법에 대해 설명할 것이다. 피셔의 정확 검정에는 fisher.test() 함수를 사용한다.
-fisher.test : 피셔의 정확 검정을 수행한다.
fisher.test(
x, # 행렬 형태의 이차원 분할표 또는 팩터
y=NULL, # 팩터. x가 행렬이면 무시된다. alternative="two.sided"
# 대립가설로 two.sided는 양측 검정, less는 작다, greater는 크다를 의미
)
MASS::survey 데이터에서 손 글씨를 어느 손으로 쓰는지와 박수를 칠 때 어느 손이 위로 가는지 사이의 경우에 대해 피셔의 정확 검정을 수행해보자. 분할표를 xtab()으로 구한 뒤 카이 제곱 검정을 수행하면 카이 제곱 검정이 정확하지 않다는 경고 메시지가 나온다.
| >xtabs(~ W.Hnd + Clap, data=survey) Clap W.Hnd Left Neither Right Left 9 5 4 Right 29 45 143 >chisq.test(xtabs(~ W.Hnd + Clap, data=survey)) Pearson's Chi-squared test data: xtabs(~ W.Hnd + Clap, data = survey) X-squared = 19.2524, df = 2, p-value = 6.598e-05 Warning message: In chisq.test(xtabs(~ W.Hnd + Clap, data = survey)) : Chi-squared approximation may be incorrect |
이 경우 fisher.test() 함수를 사용해야 한다.
| >fisher.test(xtabs(~ W.Hnd + Clap, data=survey)) Fisher's Exact Test for Count Data data: xtabs(~W.Hnd + Clap, data = survey) p-value = 0.0001413 alternative hypothesis: two.sided |
p-value가 0.05보다 작으므로 글씨를 쓰는 손과 박수를 칠 때 위에 오는 손이 독립이라는 귀무가설을 기각하고 둘 사이에 관계가 있다는 대립가설을 채택한다.
맥니마 검정
벌금을 부과하기 시작한 후 안전벨트 착용자의 수, 선거 유세를 하고 난 뒤 지지율의 변화와 같이 응답자의 성향이 사건 전후에 어떻게 달라지는지를 알아보는 경우 맥니마 검정McNemar Test을 수행한다. 사건 전후에 응답자에게 설문을 하여 사건 발생 전 설문 결과를 Test1, 사건 발생 후 설문 결과를 Test2라고 명시한 다음을 보자.
| Test 2 양성(positive) | Test 2 음성(negative) | 총계 | |
| Test 1 양성(positive) | a | b | a+b |
| Test 1 음성(negative) | c | d | c+d |
| 총계 | a+c | b+d | n |
사건 전후에 설문 결과에 응답자 수 변화가 없다면 Test1의 positive와 Test2의 positive가 동일해야 하므로 a + b = a + c가 성립해야 한다. 또한, Test1의 negative와 Test2의 negative가 동일해야 하므로 c + d = b + d가 성립해야 한다. 이 둘을 정리해 결과적으로 b = c 여부를 검토하면 사건 전후에 성향 변화가 생겼는지 알 수 있다.
b = c가 성립하려면 b, c의 값이 b + c의 절반씩이 되어야 하므로 b는 이항 분포를 따른다.

이항 분포 B(n, p)에서 n(앞서 설문 조사 표에서는 b + c에 해당)이 크다면 이항 분포를 정규 분포로 근사할 수 있다.

b를 표준화하여 N(0, 1)을 따르게 하고 연속성 수정(Continuity Correction)을 하면 다음이 성립한다.

이제 ~의 좌측에 있는 통계량을 계산한 다음 이 값이 χ2(1)의 어디에 있는지를 보면 b=c인지 여부를 알 수 있다. 이를 수행해주는 R 함수는 mcnemar.test()다. 또는 b가 b + c의 절반에 해당하는지를 이항 분포를 사용해 검정할 수도 있다. 이때 사용하는 함수는 binom.test()다.
-mcnemar.test : 맥니마 검정을 수행한다.
mcnemar.test(
x, # 행렬 형태의 이차원 분할표 또는 팩터
y=NULL, # 팩터. x가 행렬일 경우 무시
correct=TRUE # 연속성 수정 적용 여부
)
-binom.test : 이항 분포 검정을 수행한다.
binom.test(
x, # 성공의 수. 또는 성공과 실패 수를 각각 저장한 길이 2인 벡터
n, # 시행 횟수. x의 길이가 2라면 무시
p=0.5, # 성공 확률에 대한 가설
alternative=c("two.sided", "less", "greater") # 대립 가설의 형태. 기본값은 양측 검정
)
다음은 help(mcnemar.test)에서 가져온 것으로, 2×2 분할표에서 맥니마 검정을 사용하는 예다. 사용된 데이터는 투표권이 있는 나이의 미국인 1,600명에 대해 대통령 지지율을 조사한 것으로, 1차 조사(1st Survey)와 2차 조사(2nd Survey)는 한 달 간격으로 수행되었다.
| >## Agresti (1990), p. 350. >## Presidential Approval Ratings. >## Approval of the President's performance in office in two >## surveys, one month apart, for a random sample of 1600 >## voting-age Americans. >Performance<- + matrix(c(794, 86, 150, 570), + nrow = 2, + dimnames = list( + "1st Survey" = c("Approve", "Disapprove"), + "2nd Survey" = c("Approve", "Disapprove"))) >Performance 2nd Survey 1st Survey Approve Disapprove Approve 794 150 Disapprove 86 570 >mcnemar.test(Performance) McNemar's Chi-squared test with continuity correction data: Performance McNemar's chi-squared = 16.8178, df = 1, p-value = 4.115e-05 |
과에서 p-value < 0.05가 나타나 사건 전후에 Approve, Disapprove에 차이가 없다는 귀무가설이 기각된다. 즉, 사건 전후에 Approve, Disapprove 비율에 차이가 발생했다.
앞서 mcnear.test()는 이항 분포로부터 나왔으며, b가 b + c의 절반에 해당하는지를 보는 것이라고 설명했다. 따라서 binom.test()를 사용해 1차 조사에서의 Disapprove와 2차 조사에서의 Disapprove가 같은 값인지 확인할 수 있다. 다음 코드에서는 86이 86 + 150의 절반에 해당하는지를 검정하고 있다.
| >binom.test(86, 86 + 150, .5) Exact binomial test data: 86 and 86 + 150 number of successes = 86, number of trials = 236, p-value = 3.716e-05 alternative hypothesis: true probability of success is not equal to .5 95 percent confidence interval: 0.3029404 0.4293268 sample estimates: probability of success 0.3644068 |
여기에서도 p-value < 0.05로 나타나 86이 86 + 150의 절반이라는 귀무가설이 기각되었다. 즉, 사건 전후에 Approve, Disapprove 성향 차이가 발생했다.
R을 이용한 데이터 처리&분석 실무 中
'R > R을 이용한 데이터 처리&분석 실무' 카테고리의 다른 글
| 선형 회귀-1 (0) | 2020.02.06 |
|---|---|
| 상관 분석 (0) | 2020.02.06 |
| 표본 추출 (0) | 2020.02.05 |
| 기초 통계량 (0) | 2020.02.04 |
| 난수 생성 및 분포 함수 (0) | 2020.02.04 |
