좋은 모델을 만들려면 먼저 어떤 모델이 좋은 것인가부터 정해야 한다. 이 절에서는 다양한 평가 메트릭, ROC 커브, 교차 검증(Cross Validation)을 통해 모델을 평가하는 방법에 대해 알아본다.
평가 메트릭
분류가 Y, N 두 종류가 있다고 할 때 분류 모델에서의 모델 평가 메트릭(metric)은 모델에서 구한 분류의 예측값과 데이터의 실제 분류인 실제 값의 발생 빈도를 나열한 그림 9-17의 혼동 행렬(Confusion Matrix)로부터 계산한다.

혼동 행렬에서 True Positive에 해당하는 셀은 실제 값이 Y고, 예측도 Y였던 경우의 수, False Positive는 실제 값은 N이었는데 예측이 Y로 된 경우의 수를 기록한다. 같은 방식으로 False Negative와 True Negative도 기록할 수 있다.
혼동 행렬의 각 셀에 붙은 이름은 True 또는 False에 이은 Positive 또는 Negative다. 이름에서 True와 False는 예측이 정확했는지를 뜻하며, Positive와 Negative는 예측값을 의미한다. 예를 들어, True Positive는 예측이 정확했고 이때 예측값은 Positive(즉, Y)였음을 뜻한다. 또 다른 예로 False Positive는 예측이 틀렸고 예측값은 Positive였음을 뜻한다. 예측이 틀린 경우므로 실제 분류는 Negative(즉, N)다.
혼동 행렬로부터 계산할 수 있는 가장 대표적인 메트릭은 표 9-11을 참고하기 바란다.

예측 결과가 담긴 predicted 벡터와 이들의 실제 분류가 담긴 actual 벡터를 정의하고 위에서 설명한 메트릭을 계산해보자.
| > predicted<-c(1, 0, 0, 1, 1, 1, 0, 0, 0, 1, 1, 1) > actual<-c(1, 0, 0, 1, 1, 0, 1, 1, 0, 1, 1, 1) |
분할표를 사용해 그림 9-17과 같이 표현한다.
| > xtabs( ~ predicted + actual) actual predicted 0 1 0 3 2 1 1 6 |
이 표를 통해서 예측 결과와 실제 결과가 일치하는 경우와 그렇지 않은 경우를 쉽게 알 수 있다. Accuracy는 예측값 중 올바른 값의 비율로 다음과 같이 계산한다.
| > sum(predicted == actual) / NROW(actual) [1] 0.75 |
이렇게 모든 경우를 하나하나 코드를 작성해 계산할 수도 있겠지만 caret의 confusionMatrix( )를 사용하면 손쉽게 정리된 결과를 얻을 수 있다.
-caret::confusionMatrix : 혼동 행렬과 관련된 메트릭을 계산한다.
caret::confusionMatrix(
data, # 예측값 또는 분할표
reference # 실제 값
)
다음은 predicted와 actual에 대해 confusionMatrix()를 호출한 결과다. 분할표뿐만 아니라 다양한 평가 메트릭이 한 번에 계산되는 것을 볼 수 있다.(※ 바로 confusionMatrix에 predicted, actual을 입력했을 때 에러가 나서 이들을 factor로 바꿔준 뒤 실행하였다.)
| >confusionMatrix(predicted, actual) >f_predicted <- as.factor(predicted) >f_actual <- as.factor(actual) >confusionMatrix(f_predicted, f_actual) >install.packages("e1071") >library(e1071) >confusionMatrix(f_predicted, f_actual) |
위 결과에서 No Information Rate에 대해서만 추가로 살펴보자. No Information Rate는 가장 많은 값이 발견된 분류의 비율이다. 이 예의 Reference(실제 값)에는 0이 4개, 1이 8개 있었다. 이런 데이터가 주어졌을 때 가장 간단한 분류 알고리즘은 입력이 무엇이든 항상 1을 출력하는 것이다. 데이터에서 분류 1의 비율이 분류 0의 비율보다 높으므로 정확도가 50%는 넘을 것이기 때문이다. 항상 1을 결과로 출력하는 분류 알고리즘의 정확도는 8/(4+8)=0.6667이며 No Information Rate는 바로 이 값에 해당한다.
실제 분류 알고리즘은 피처를 들여다보고 예측을 수행하므로 분류의 비율만 보고 결과를 출력하는 단순한 분류 알고리즘보다 성능이 좋아야 한다. 따라서 0.6667은 모델을 만들었을 때 무조건 넘어야 하는 정확도다.
ROC 커브
많은 기계 학습 모델은 그 내부에서 결과가 Y일 확률 또는 점수를 계산한다. 그리고 점수가 특정 기준을 넘으면 Y로, 기준을 넘지 않으면 N으로 예측값을 출력한다. 예를 들어, 표 9-13과 같이 각 관측값에 대한 점수가 주어졌다고 하자.

표 9-13에서 점수의 기준값을 0.7로 놓으면 #3, #7, #2, #15는 Y로 #6은 N으로 예측된다. 기준값을 0.8로 하면 #3, #7만 Y로 예측된다.
ROC 커브는 점수 기준을 달리할 때 TP Rate와 FP Rate가 어떻게 달라지는지 그래프로 표시한 것이다. 표 9-13의 데이터에 실제 분류를 추가하면 표 9-14가 된다.

표 9-14와 같은 데이터가 있을 때 예측을 Y로 판단하는 기준값이 관측값 #3과 같다면 TP Rate는 1/3, FP Rate는 0이다. 기준값이 #7과 같았다면 TP Rate는 2/3, FP Rate는 0이다. 이를 정리하면 표 9-15와 같다.
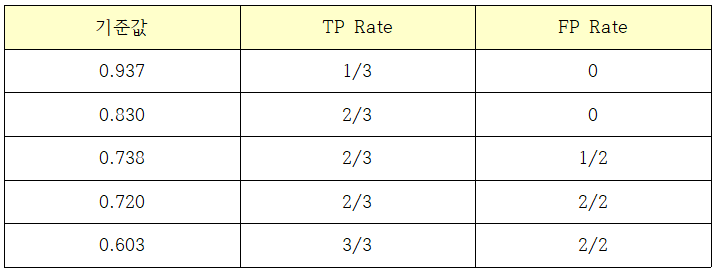
표 9-15를 X 축을 FP Rate, Y축을 TP Rate로 한 좌표 평면에 그린 것이 그림 9-18에 보인 ROC 커브다.
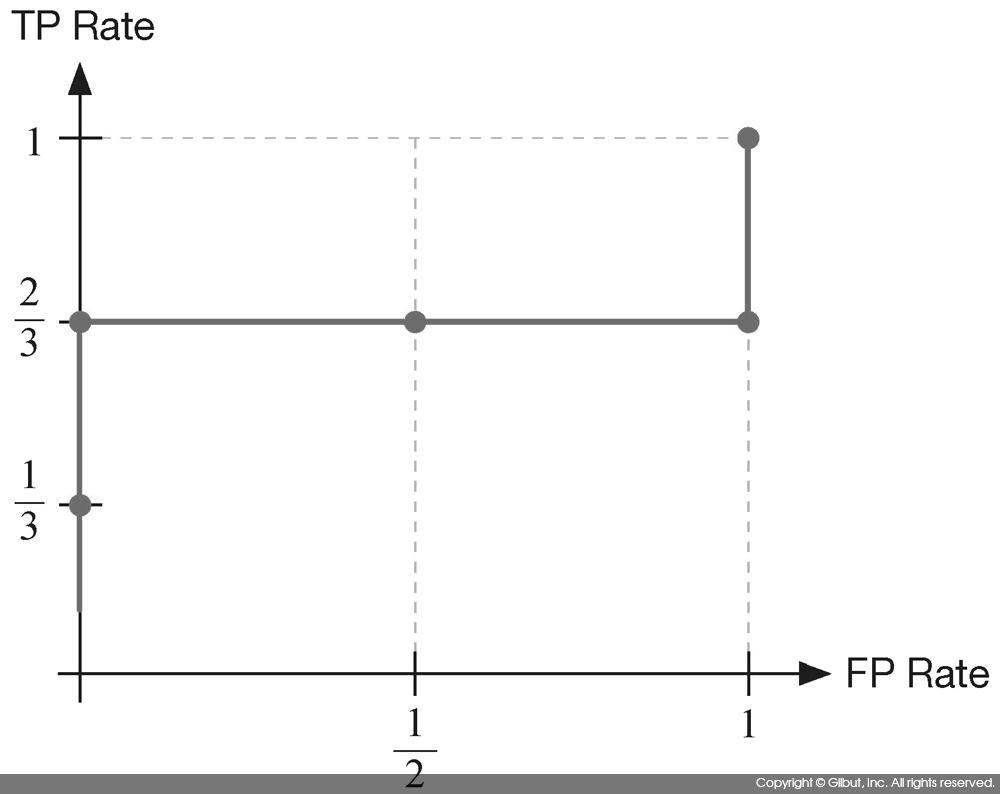
이처럼 ROC 커브는 FP Rate 대비 TP Rate의 변화를 뜻한다. 따라서 그림 9-19에 보인 것처럼 TP Rate가 1로 한 번에 올라간 뒤 FP Rate가 뒤따라 증가하는 형태가 가장 이상적이다. 이런 형태는 실제로 Y인 결과에 높은 점수를 주는 모델을 뜻한다.

ROC 커브를 사용하면 두 개의 모델을 비교할 수 있다. 그림 9-20에 보인 모델 (A)와 모델 (B)를 보자. 모델 (B)는 모델 (A)에 비해 FP Rate 대비 TP Rate가 컸다. 따라서 모델 (B)가 모델 (A)보다 우수하다. 일반적으로는 ROC 커브를 그린 뒤 좌측 상단에 위치한 커브가 더 우수한 것으로 보면 된다.

이러한 이유로 ROC 커브를 그린 뒤 그 아래의 면적을 AUC(Area Under the Curve)라 하여 모델 간의 비교에 사용한다. 그림 9-21에 AUC를 보였다.

여기서는 ROCR 패키지를 사용하여 ROC 커브를 그리는 방법에 대해 살펴본다. 다음은 ROC 커브 관련 함수를 정리한 것이다.
-ROCR::prediction : prediction 객체를 생성한다.
ROCR::prediction(
predictions, # 예측값
lables # 실제 값
)
-ROCR::performance : prediction 객체로부터 performance 객체를 생성한다.
ROCR::performance(
prediction.obj, # prediction 객체
# 성능 평가 메트릭. acc(Accuracy), fpr(FP Rate), tpr(TP Rate), rec(recall) 등을 지정할 수 있다.
# 전체 목록은 도움말 ?performance를 참고하기 바란다.
measure,
# 두 번째 성능 평가 메트릭. x.measure를 지정하면 X 축은 x.measure, Y 축은 measure에 지정한
# 메트릭으로 그래프를 그린다. x.measure를 지정하지 않으면 기본값 "cutoff"가 사용된다.
# cutoff는 표 9-15를 설명하면서 사용한 기준값에 해당한다. 즉, 서로 다른 기준값에 대한
# measure의 그래프가 그려지게 된다.
x.measure="cutoff",
... # 성능 메트릭에 추가로 넘겨줄 인자들
)
설명을 위해 다음과 같이 예측값과 실제 분류가 주어졌다고 가정해보자. probs는 분류 알고리즘이 예측한 점수고, labels는 실제 분류(true class)가 저장된 벡터다. labels 내의 ifelse는 약간의 분류 실패를 시뮬레이션해본 것이다. set.seed( )는 난수 생성기의 시드(seed)를 지정하기 위해 사용했다. 난수 생성기가 생성하는 난수는 시드에 의해 좌우되므로 예제 코드와 같은 시드를 지정하면 독자들도 이 책에서 보인 것과 동일한 결과를 얻을 수 있다.
| > set.seed(137) > probs<-runif(100) > labels<-as.factor(ifelse(probs>.5&runif(100)<.4,"A","B")) |
ROCR을 사용하기 위해 prediction 객체를 만든다.
| > install.packages("ROCR") > library(ROCR) > pred <- prediction(probs, labels) |
prediction 객체를 performance( ) 함수에 넘겨 tpr, fpr을 구하고 ROC 커브를 그려보도록 하자.
| > plot(performance(pred, "tpr", "fpr")) |
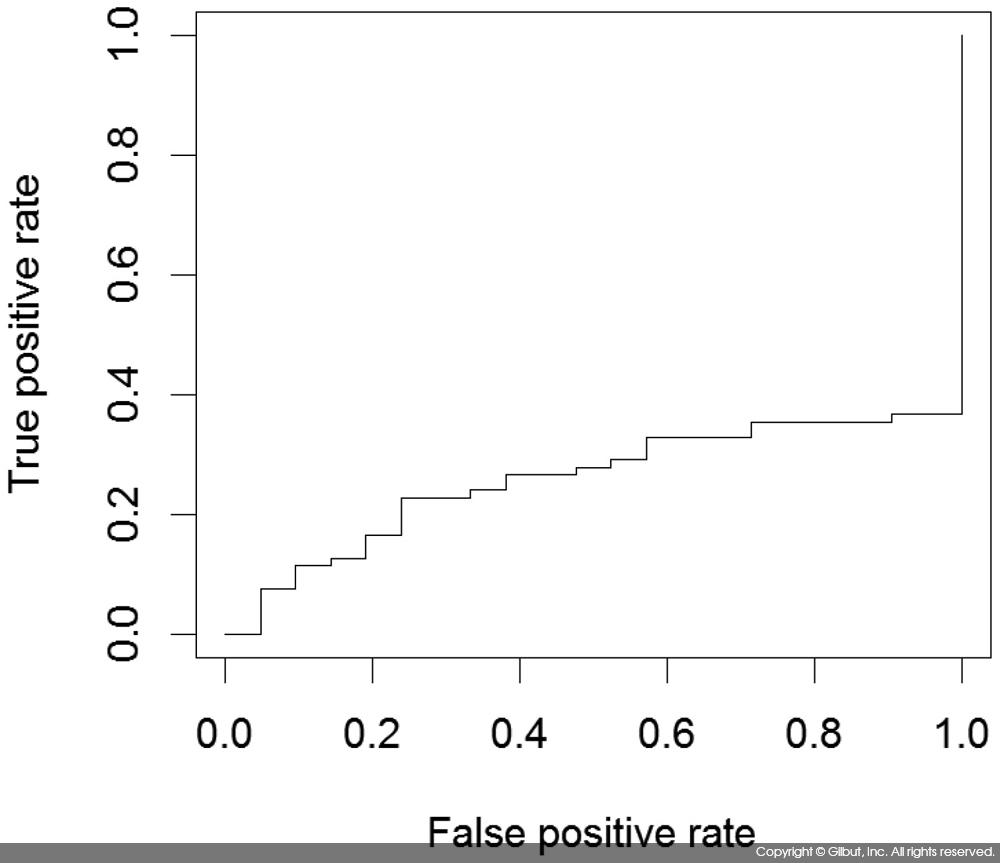
마찬가지로 acc, cutoff를 인자로 지정하면 cutoff 값(표 9-15에서 설명한 기준값)에 따른 Accuracy의 변화를 볼 수 있다.
| > # x.measure의 기본값이 cutoff므로 plot(performance(pred, "acc"))로 해도 결과는 같다. > plot(performance(pred, "acc", "cutoff")) |
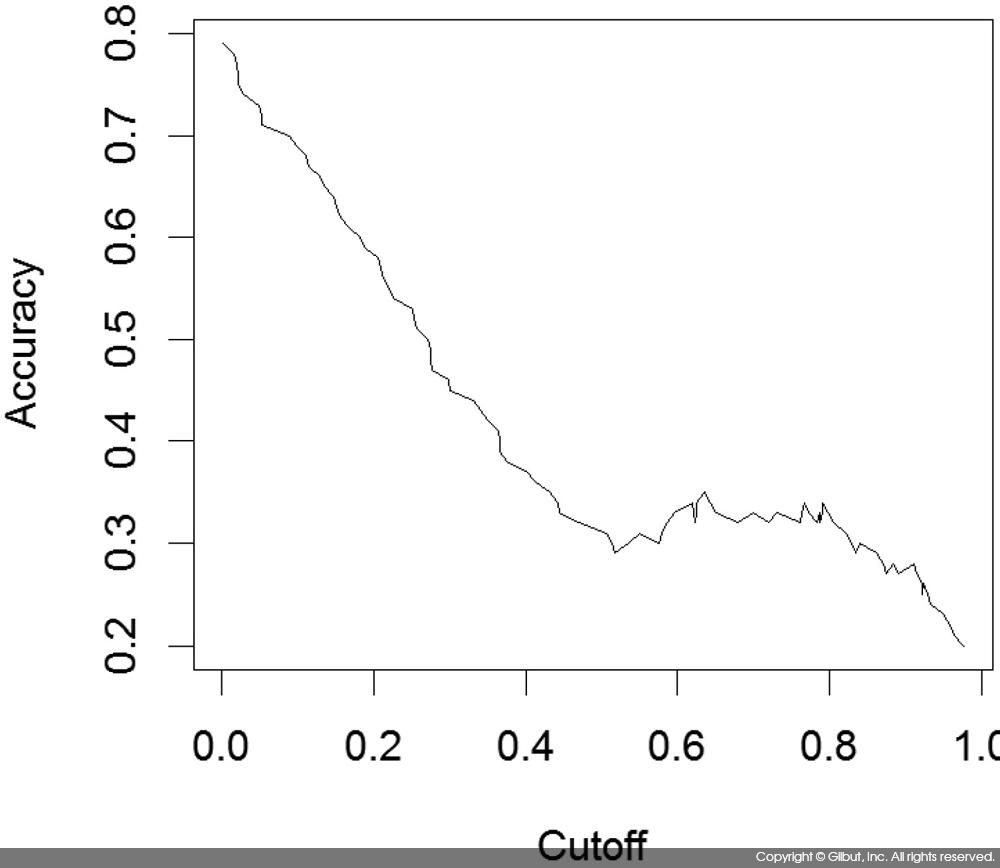
AUC(Area Under the Curve)는 auc 인자를 지정하고 y.values를 보면 된다.
| > performance(pred, "auc") An object of class "performance" Slot "x.name": [1] "None" Slot "y.name": [1] "Area under the ROC curve" Slot "alpha.name": [1] "none" Slot "x.values": list() Slot "y.values": [[1]] [1] 0.2579867 Slot "alpha.values": list() |
위 코드의 실행 결과 AUC는 0.2579867로 나타났다.
R을 이용한 데이터 처리&분석 실무 中
'R > R을 이용한 데이터 처리&분석 실무' 카테고리의 다른 글
| 로지스틱 회귀 모델 (0) | 2020.02.12 |
|---|---|
| 모델 평가 방법 - 2 (0) | 2020.02.11 |
| 전처리-2 (0) | 2020.02.10 |
| 전처리-1 (0) | 2020.02.09 |
| 데이터 탐색 (0) | 2020.02.09 |
