예측하고자 하는 분류가 두 개가 아니라 여러 개가 될 수 있는 경우 다항 로지스틱 회귀 분석(Multinomial Logistic Regression)을 사용한다. 이 방법의 기본 아이디어는 로지스틱 회귀 분석을 확장하는 것이다. 이 절에서는 위키피디아에 설명된 독립 바이너리 회귀의 집합에 따라 모델을 설명한다.
분류 K를 기준으로 하여 데이터가 각 분류에 속할 확률을 β_(i)X_(i)로 놓는다.
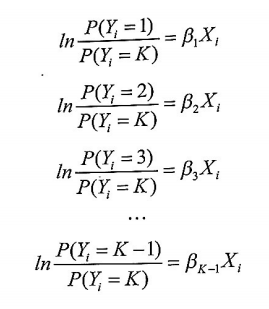
양변을 e의 지수로 하고 정리하면 다음과 같다.

확률의 합은 1이므로 위 식의 좌변과 우변을 모두 합하면 다음과 같다.

이를 정리하면 P(Yi = K를 다음과 같이 구할 수 있다.

최종적으로 i < K인 경우는 P(Yi = i)는 다음과 같다.

R에서는 nnet::multinom( )을 사용해 다항 로지스틱 회귀 모델을 작성할 수 있다.
-nnet::multinom : 다항 로지스틱 회귀 모델을 생성한다.
nnet::multinom(
formula, # 모델 포뮬러
data, # 포뮬러를 적용할 데이터
)
-fitted : 모델에 의해 훈련 데이터가 어떻게 적합(fit)되었는지 보인다.
fitted(
object # 모델
)
기계 학습 모델은 훈련 데이터에 대한 분류 예측을 잘 수행하도록 파라미터를 수정해가면서 만들어진다. 이를 모델이 훈련 데이터에 적합된다고 말한다. fitted( )의 반환 값은 모델이 훈련 데이터에 어떻게 적합되었는지 보여주는 값들이다.
-predict.multinom : 다항 로지스틱 회귀 모델을 사용한 예측을 수행한다.
predict.multinom(
object, # multinom() 함수로 생성한 nnet 객체
newdata, # 예측을 수행할 데이터
# 예측 결과의 유형. class는 분류를, probs는 각 분류일 확률을 반환한다. 기본값은 class다.
type=c("class", "probs")
)
아이리스의 Species에 대해 모델을 작성해본다.
> library(nnet)
> (m<-multinom(Species ~., data=iris))
# weights: 21 (12 variable)
initial value 164.791843
iter 10 value 23.871380
iter 20 value 6.199521
iter 30 value 5.978767
iter 40 value 5.957688
iter 50 value 5.948645
final value 5.948287
converged
Call:
multinom(formula = Species ~ ., data = iris)
Coefficients:
(Intercept) Sepal.Length Sepal.Width Petal.Length Petal.Width
versicolor 14.95244 -3.920396 -6.812452 12.29256 -1.322394
virginica -26.72947 -6.416181 -13.422147 21.54193 16.804063
Species2
versicolor -3.736148
virginica -3.610014
Residual Deviance: 11.89657
AIC: 35.89657
작성한 모델이 주어진 훈련 데이터에 어떻게 적합되었는지는 fitted( )를 사용해 구할 수 있다.
> head(fitted(m))
setosa versicolor virginica
1 0.9999998 1.555649e-07 5.858452e-34
2 0.9999998 2.449906e-07 4.697407e-32
3 0.9999983 1.685300e-06 4.961148e-32
4 0.9999986 1.373817e-06 7.251856e-31
5 0.9999999 1.164961e-07 2.907486e-34
6 1.0000000 2.300452e-09 1.988838e-34fitted( )의 결과는 각 행의 데이터가 각 분류에 속할 확률을 뜻한다. 어떤 분류로 예측되었는지를 알아내기 위해 각 행마다 가장 큰 값이 속하는 열을 뽑을 수도 있겠지만, 더 간단하게 predict( )를 사용해도 된다. 특히 predict( )에는 newdata에 새로운 데이터를 지정할 수 있으므로 새로운 관측값에 대한 예측을 수행하려면 predict( )를 사용해야 한다.
setosa, versicolor, virginica에서 한 행씩 뽑아 predict( )를 적용해보자. 분류를 얻을 때는 type=“class”를 지정해야 하지만, type의 기본값이 class므로 생략해도 된다.
> predict(m, newdata=iris[c(1, 51, 101), ], type="class")
[1] setosa versicolor virginica
Levels: setosa versicolor virginica
각 분류에 속할 확률을 예측하고자 한다면 predict( ) 사용 시 type=“probs”를 지정한다.
> predict(m, newdata=iris, type="probs")
setosa versicolor virginica
1 9.999998e-01 1.555649e-07 5.858452e-34
2 9.999998e-01 2.449906e-07 4.697407e-32
3 9.999983e-01 1.685300e-06 4.961148e-32
4 9.999986e-01 1.373817e-06 7.251856e-31
5 9.999999e-01 1.164961e-07 2.907486e-34
6 1.000000e+00 2.300452e-09 1.988838e-34
7 9.999981e-01 1.912688e-06 2.976774e-31
...
모델의 정확도는 예측된 Species와 실제 Species를 비교하여 알 수 있다. 예측값을 predicted에 저장하고 이 중 iris$Species와 같은 경우의 비율을 세서 정확도를 계산해보자.
> predicted <- predict(m, newdata=iris)
> sum(predicted == iris$Species) / NROW(predicted)
[1] 0.9866667
아이리스처럼 대상으로 하는 분류의 개수가 2개 이상인 경우에는 분할표를 사용해 세부적인 예측 정확도를 분석할 수 있다.
> xtabs(~ predicted + iris$Species)
iris$Species
predicted setosa versicolor virginica
setosa 50 0 0
versicolor 0 49 1
virginica 0 1 49
표를 통해 총 2개의 예측이 잘못되었고, versicolor를 virginica로 예측한 경우가 1건, virginica를 versicolor로 예측한 경우가 1건 있었음을 알 수 있다. 그러나 여기서 구한 정확도는 훈련 데이터에 대해서 직접 계산한 것이므로, 새로운 데이터에 대한 예측 성능으로 활용할 수는 없음을 기억하기 바란다.
R을 이용한 데이터 처리&분석 실무 中
'R > R을 이용한 데이터 처리&분석 실무' 카테고리의 다른 글
| 신경망 (0) | 2020.02.12 |
|---|---|
| 의사 결정 나무 (0) | 2020.02.12 |
| 로지스틱 회귀 모델 (0) | 2020.02.12 |
| 모델 평가 방법 - 2 (0) | 2020.02.11 |
| 모델 평가 방법 (0) | 2020.02.11 |


