신경망(Neural Network)은 인간의 뇌를 본 따서 만든 모델이다. 신경망에는 뉴런을 흉내 낸 노드들이 입력층(Input Layer), 은닉층(Hidden Layer), 출력층(Output Layer)으로 구분되어 나열되어 있다. 입력층에 주어진 값은 입력층, 은닉층, 출력층 순서로 전달된다.
신경망은 예측 성능이 우수하다고 알려져 있다. 특히 은닉층에서 입력 값이 조합되므로 비선형적인 문제를 해결할 수 있는 특징이 있다. 그러나 의사 결정 나무 등의 모델과 비교해 만들어진 모델을 직관적으로 이해하기가 어렵고 수작업으로 모델을 수정하기도 어렵다.
신경망 모델
그림 10-7에 신경망 모델의 개념도를 보였다.

신경망에 입력이 주어지면 그 값은 그림 10-7에 보인 화살표를 따라 전달되어 은닉층에 도달한다. 은닉층의 노드는 주어진 입력에 따라 활성화된다. 활성화된 은닉 노드는 출력 값을 계산하고 그 결과를 출력층에 전달한다. 출력층의 노드는 입력에 따라 활성화되고, 활성화된 노드들이 최종 출력 값을 계산한다. 이 출력 값이 모델의 최종 예측 결과가 된다.
각 화살표에는 가중치(연결 강도)가 부여된다. 입력층의 노드 i와 은닉층의 노드 j를 연결한 화살표에 부여된 가중치를 w_(ji)라 하고, 입력층에 오는 입력을 x_1, x_2, …, x_i, …, x_n이라 하자. 그러면 입력층에 주어진 값들은 은닉층 노드 j로 다음과 같이 모인다.

노드 j로 전달되는 이 값을 넷 활성화(net activation)라 하고, 이와 같은 계산식을 합성 함수(combination function)라고 한다.
은닉층 노드 j가 출력층에 보내는 값은 넷 활성화 값을 활성 함수(activation function)에 통과시킨 결과다. 활성 함수 중 많이 사용되는 두 가지를 소개한다. 식 10-3은 부호(sign)에 따라 다른 결과를 출력하는 함수고, 식 10-4는 시그모이드(sigmoid) 함수다.

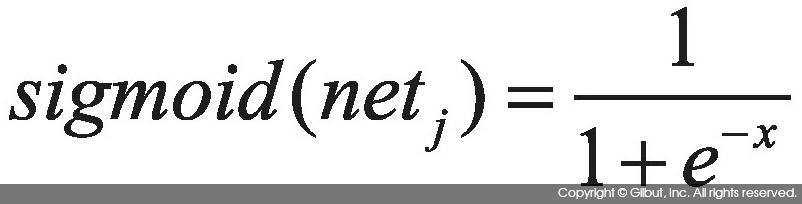
시그모이드 함수는 그림 10-8에 보인 것과 같이 0 ~ 1 사이의 출력을 내보내는 함수다. x 값이 작은 영역에서는 입력에 민감하게 출력이 크게 변하고, x 값이 큰 영역에서는 입력에 덜 민감하게 출력이 변한다.

신경망 학습은 가중치 w의 조절 작업이다. 입력 값 X와 원하는 출력 값 Y가 있을 때 입력 값을 입력층에 준 다음, 모델의 출력 값이 원하는 출력 값과 같은지를 확인한다. 값이 같지 않다면 가중치 w를 적절히 조절한다.
모델의 출력 값이 원하는 출력 값과 얼마나 같은지를 비교하는 기준에는 에러의 제곱 합(SSE, Sum of Squared Error)과 정보 이론의 엔트로피가 있다. 출력층 노드 i의 출력 값이 hat(y_(i)), 원하는 출력 값이 y_i라 할 때 SSE는 식 9-5와 같다.

식 10-5에서 차이가 발견되면 (즉, 식 10-5가 0이 아니면) 차이가 발생한 출력 노드로부터 해당 출력 노드에 연결된 은닉 노드로, 은닉 노드에서 입력 노드로 거슬러 올라가면서 가중치를 조절하여 식 10-5가 0에 가까워지도록 한다. 이를 수회 반복하다 보면 적절한 가중치가 발견된다. 이 학습 방법을 역전파 알고리즘Back Propagation Algorithm이라 한다. 역전파 알고리즘은 홉필드Hopfield가 개발한 것으로, 이 알고리즘의 개발 덕분에 신경망 모델이 널리 사용되게 되었다.
신경망 모델의 학습 과정에서 주어진 데이터에 딱 맞게 가중치를 조절하다 보면 과적합이 발생할 수 있다. 과적합을 피하는 한 가지 방법은 역전파 알고리즘에 따라 가중치를 교정할 때마다 0과 1 사이의 값을 가지는 ε을 가중치에 곱해주는 것이다. 이를 가중치 감소weight decay라 한다.
w = w × (1-ε) (식 10-6)
신경망의 출력으로 확률을 원할 경우 최솟값이 0, 최댓값이 1이 되도록 해주는 소프트맥스 함수를 사용한다. 식 10-7은 출력 노드 k의 넷 활성화가 netk일 때 노드 k의 소프트맥스를 구하는 식이다.

이상으로 신경망 모델에 대해 살펴봤다. 더 자세한 내용은 이 절을 설명하면서 사용한 참고자료를 보기 바란다.
신경망 모델 학습
R의 nnet 패키지는 신경망 모델 작성을 위한 함수다. nnet 패키지에서 신경망의 파라미터는 엔트로피(entropy) 또는 SSE(Sum of Squared Error)를 고려해 최적화된다. 출력 결과는 소프트맥스(softmax)를 사용해 확률과 같은 형태로 변환할 수 있다. 과적합을 막기 위한 방법으로 가중치 감소(weight decay)를 제공한다.
-nnet::nnet : 신경망 모델을 생성한다.
nnet::nnet(
formula, # 모델 포뮬러
data, # 포뮬러를 적용할 데이터
weights, # 데이터에 대한 가중치
...
)
nnet::nnet(
x, y, # 데이터
weights, # 데이터에 대한 가중치
size, # 은닉층 노드의 수
Wts, # 초기 가중치 값. 생략할 경우 임의의 값이 가중치로 할당된다.
mask, # 최적화할 파라미터. 기본값은 모든 파라미터의 최적화다.
# TRUE면 활성 함수로 y=ax+b 같은 유형의 선형 출력(linear output)이 사용된다.
# FALSE면 로지스틱 함수(즉, 시그모이드 함수)가 활성 함수로 사용된다.
linout=FALSE,
# 모델 학습 시 모델의 출력과 원하는 값을 비교할 때 사용할 함수. TRUE면 엔트로피,
# FALSE면 SSE가 사용된다.
entropy=FALSE,
# 출력에서 소프트맥스 사용 여부
softmax=FALSE,
# 가중치의 최대 개수로 기본값은 1000. 모델이 복잡해 가중치의 수가 많다면 이 값을 증가시켜야 한다.
MaxNWts = 1000
)
-nnet::predict.nnet : nnet을 사용한 예측을 수행한다.
nnet::predict.nnet(
object, # nnet 객체
newdata, # 예측을 수행할 데이터
# 예측 결과의 유형. raw는 신경망이 반환하는 행렬. class는 예측된 분류
type=c("raw", "class")
)
포뮬러를 사용한 모델 생성
신경망을 잘 사용하려면 데이터에 정규화를 적용한 뒤 신경망 모델을 만들어야 한다. 정규화가 절대적인 의무 사항은 아니지만 정규화를 적용하면 지역 해에 빠질 위험을 피한다.
아래 예에서는 정규화 과정 없이 아아리스 데이터에 대한 신경망 모델을 만들었다.
> library(nnet)
> m <- nnet(Species ~., data=iris, size=3) # 은닉층 노드 수 = 3
# weights: 27
initial value 209.776713
iter 10 value 68.839766
iter 20 value 68.325309
iter 30 value 48.408527
iter 40 value 11.403077
iter 50 value 7.095460
iter 60 value 6.106387
iter 70 value 5.988069
iter 80 value 5.965337
iter 90 value 5.959421
iter 100 value 5.958498
final value 5.958498
stopped after 100 iterations
아이리스 데이터 자신에 대한 예측 결과는 다음과 같다.
> predict(m, newdata=iris)
setosa versicolor virginica
1 9.999874e-01 1.263331e-05 3.959453e-28
2 9.999588e-01 4.118988e-05 7.729874e-27
3 9.999766e-01 2.335103e-05 1.855355e-27
4 9.999421e-01 5.786730e-05 1.817189e-26
5 9.999888e-01 1.119066e-05 2.918959e-28
...
146 8.955349e-19 1.350138e-05 9.999865e-01
147 1.310257e-15 1.087811e-03 9.989122e-01
148 1.559853e-15 1.208206e-03 9.987918e-01
149 4.507296e-19 8.928967e-06 9.999911e-01
150 2.071929e-13 2.276016e-02 9.772398e-01
만약 모델로부터 예측된 분류를 바로 얻고자 한다면 다음과 같이 type에 class를 지정한다.
> predict(m, newdata=iris, type="class")
지금까지 보인 방법은 nnet( )에 포뮬러를 지정한 형태였다. 포뮬러를 지정할 경우 nnet( )은 다음과 같이 동작하도록 되어 있다.
1. linout의 기본값이 FALSE므로 출력층에서 선형 함수가 아니라 시그모이드 함수가 사용된다.
2. 예측 대상이 되는 분류(즉, Y의 레벨)의 수가 2개라면 엔트로피를 사용해 파라미터가 추정된다. 분류의 수가 3개 이상이라면 SSE(Sum of Squared Errors)로 파라미터가 추정되며 소프트맥스가 적용된다.
X와 Y의 직접 지정
좀 더 빠른 속도를 원하거나 각종 파라미터가 nnet( )에서 자동으로 지정되는 것을 원치 않는 경우 X, Y를 지접 지정하는 형태로 nnet( )을 호출할 수도 있다. 이를 위해 가장 먼저 할 일은 Y를 지시 행렬(Indicator Matrix)로 변환하는 것이다.
-nnet::class.ind : 주어진 분류(클래스)에 대한 지시 행렬을 만든다.
nnet::class.ind(
cl # 팩터 또는 분류(class)의 벡터
)
다음은 아이리스의 Species에 대한 지시 행렬을 만든 예다. setosa, versicolor, virginica가 각각의 컬럼으로 되어 있으며 데이터가 해당 분류에 속하는 경우 컬럼 값이 1이다.
> class.ind(iris$Species)
setosa versicolor virginica
[1,] 1 0 0
[2,] 1 0 0
[3,] 1 0 0
[4,] 1 0 0
[5,] 1 0 0
...
[51,] 0 1 0
[52,] 0 1 0
[53,] 0 1 0
[54,] 0 1 0
[55,] 0 1 0
...
[101,] 0 0 1
[102,] 0 0 1
[103,] 0 0 1
[104,] 0 0 1
[105,] 0 0 1
...
이제 X에는 iris에서 Species를 제외한 나머지 변수들을 지정하고, Y에 class.ind( )의 결과를 지정하면 X, Y를 직접 지정한 nnet( )이 호출된다.
> m2 <- nnet(iris[, 1:4], class.ind(iris$Species), size=3,
+ softmax=TRUE)
# weights: 27
initial value 179.822518
iter 10 value 69.476514
iter 20 value 65.407837
iter 30 value 13.239150
iter 40 value 6.182978
iter 50 value 5.988953
iter 60 value 5.964934
iter 70 value 5.960658
iter 80 value 5.960084
iter 90 value 5.958269
iter 100 value 5.956502
final value 5.956502
stopped after 100 iterations
> predict(m2, newdata=iris[, 1:4], type="class")
[1] "setosa" "setosa" "setosa" "setosa" "setosa" ...
R을 이용한 데이터 처리&분석 실무 中
'R > R을 이용한 데이터 처리&분석 실무' 카테고리의 다른 글
| 클래스 불균형 (0) | 2020.02.13 |
|---|---|
| 서포트 벡터 머신 (0) | 2020.02.13 |
| 의사 결정 나무 (0) | 2020.02.12 |
| 다항 로지스틱 회귀 분석 (0) | 2020.02.12 |
| 로지스틱 회귀 모델 (0) | 2020.02.12 |


